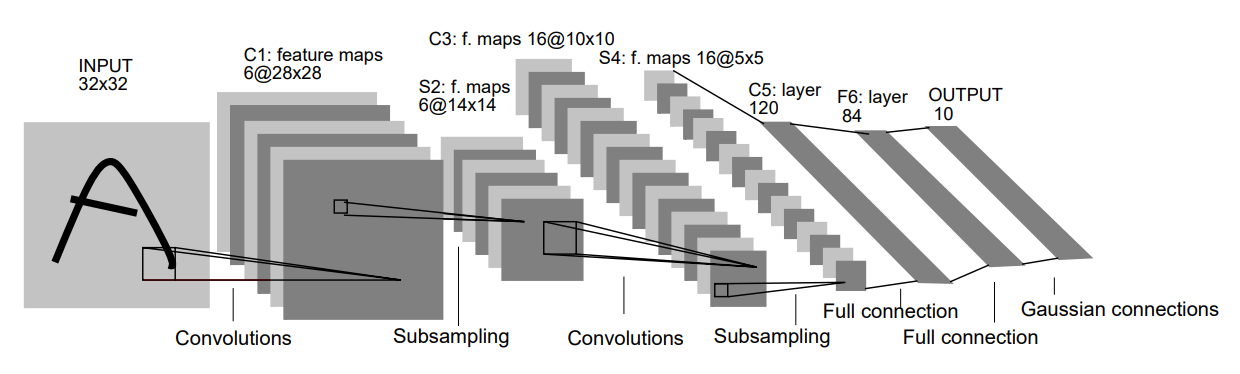
What is Convolutional Neural Network?
A Convolutional Neural Network (CNN) is a class of Artificial Neural Networks (ANN). This kind of neural networks use “Convolution” in place of “A general matrix multiplication” in at least one of their layers. A convolution layer performs sparse interactions, parameter sharing, and equivalent representations. Fully connected layer does not have above-mentioned characteristics. Due to these ability of convolution layer, it can extract features efficiently from high dimensional data such as images by focusing at local regions instead of looking at the whole image.
Convolution Operation in Convolutional Neural Network:
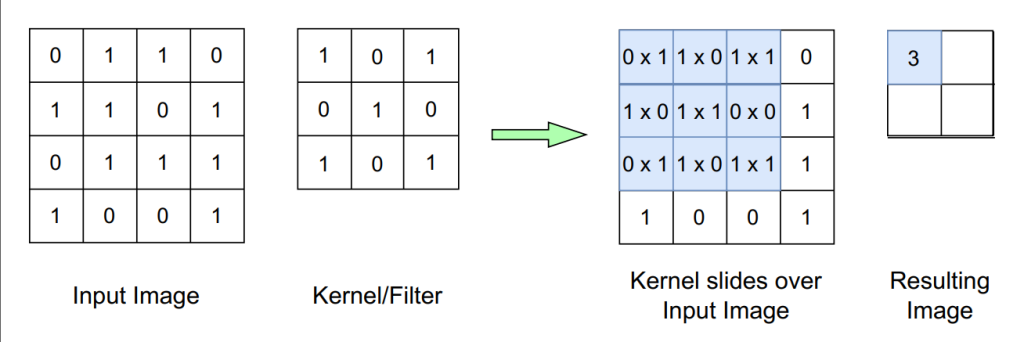
The convolution operation in a convolution layer is shown in the above Figure. When the image data in form of pixels enters in a convolution layer, each kernel slides over input data spatially, and the layer performs convolution operation. In this process, each value of a kernel multiplies with the respective pixel value when it slides over the data, and generates a scalar product.
All scalar products of kernel’s value and data are then added to produce one pixel value of 2D activation map. This way a kernel can see a specific feature at a specific pixel position in the image. Corresponded 2D activation maps of all kernels adds themselves up. Thus, a complete output generates. The depth, the stride, and the padding are the parameters help in optimizing the feature extraction procedure in a convolution layer. The following sections explains these parameters in brief.
Convolution Filters:
Convolution filters are learnable kernels. These filters are responsible to detect a specific feature from the input data. Additionally, as explained in above section, these kernels spread along all dimensions of the input and form activation maps. Instead of using default initialization for kernel value in convolution layer, one can use different kernels with different layers to extract specific features.
What is Stride and Depth in a Convolutional Neural Network?
Stride:
Stride is the unit/units a kernel glides over the input image from one position. As the stride increases, the compression of image/video data happen to a greater extent. In other words, a smaller stride number gives greater number of activation maps, and vice versa. The output dimension of a convolution layer in any CNNs without the padding feature can be determined using the following equation.
Convolution Output Dimension = ( ( I – K ) / S ) + 1
where, I is the input dimensions of the image (height * width * depth), K is the size of kernel, S is the stride.
Depth:
The depth is the number of kernels in a convolution layer gliding over the input data in a spatial dimension. It represents the output volume given by a convolution layer. A smaller number of the depth leads to minimization of total number of neurons in the network, and simultaneously reduces the capability of feature extraction.
Padding in a CNN Layer:
Zero-padding feature of any CNNs controls the dimensionality of the output size. Moreover, there are two ways to control it. One way is to reduce the dimensionality of the output size. Also, the other way is to maintain the dimensionality to the original output size or to required extent. Without zero-padding the input data, any kernel can only visit the border’s pixels one time, and the size of the output shrinks by some pixels at each layer of CNNs. Using this feature, the width of the kernel and output size independently and effectively stay in limits. The output dimension of a convolution layer in any CNNs with the padding feature can be determined using the following equation.
Convolution Output Dimension = ( ( I – K + 2P ) / S ) + 1
where, I is the input dimensions of the image (height x width x depth), K is the size of kernel, P is the amount of zero padding, S is the stride.
References:
- Yann LeCun et al. “Gradient-based learning applied to document recognition”. In: Proceedings of the IEEE 86.11 (1998), pp. 2278–2324.